今回のまとめ

このページでは、固体および気体が溶媒に溶解する様子について解説していきます。溶解においては、固体が溶けるのか気体が溶けるのかで使う公式が異なります。したがって、ぞれぞれの場合に分けて検討していきましょう。気体の溶解においては、ヘンリーの法則を上手く使うことが大切です。一方、固体の溶解では溶解度の計算ができるようにしておきましょう。この後でそれぞれを詳しく学習していきます。
溶解の法則
まず初めに、溶解の法則について学習します。溶媒には極性分子からなる極性溶媒と、無極性分子からなる無極性溶媒があります。それぞれの例としては、極性溶媒では水、無極性溶媒ではジエチルエーテルなどが挙げられます。
極性溶媒は極性物質をよく溶かし、無極性溶媒は無極性溶媒をよく溶かすという性質があります。これは、極性をもつ分子は静電気力によって引き付けあう一方で、無極性の物質とは混ざり合わない性質を持っているからです。つまり、似た性質をもつ溶媒に溶解すると覚えておきましょう。
気体の溶解度
溶解度の定義

気体の溶解度は、1atm下で水1Lに溶ける気体の体積を標準状態(0℃、1atm)に換算して表されます。ただし、この定義はあまり厳密には用いられていないので、参考程度に覚えておきましょう。気体の溶解度は、温度が上がることで減少することが知られています。
ヘンリーの法則
気体の溶解を考える上で、ヘンリーの法則は非常に重要です。ヘンリーの法則とは、気体の溶解量(mol)は、気体の分圧と溶媒の体積に比例するというものです。厳密にはヘンリーの法則は分圧に関しての記述のみですが、問題を解く上では溶媒量にも比例することを覚えておく必要があります。
ヘンリーの法則を扱う際には、気体の物質量が比例することに注意しましょう。通常、気体の量を表す際には体積で表現されることが多いので、これを物質量に直してヘンリーの法則を適用する必要があります。
気体の溶解(体積で比較)
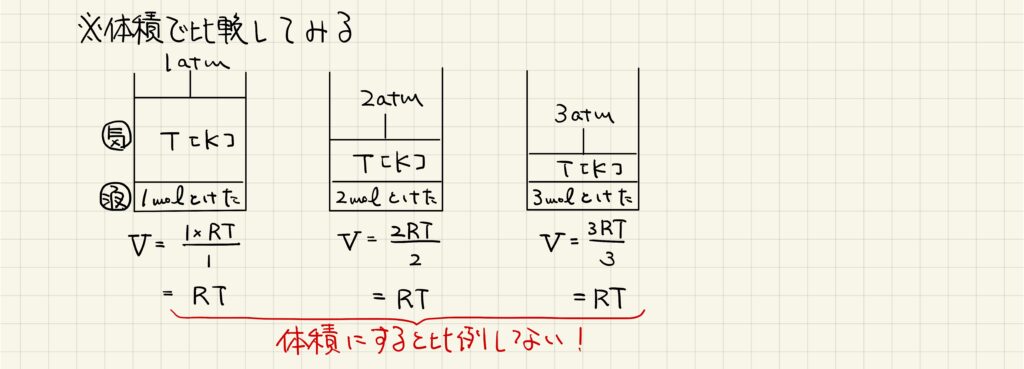
では、気体の体積ベースで比較するとどのようになるか見ていきましょう。一番左の図を基準として考えると、1Lの水に気体が1mol溶けていることになります。ここで圧力を2倍、3倍としていくと、ヘンリーの法則により気体の物質量も2倍、3倍溶解します。しかし、これを体積に直すと、どれも同じ量になってしまいます。体積に換算すると比例しないので、ヘンリーの法則では必ず気体の物質量で計算するようにしましょう。
固体の溶解
溶解度の定義

次に、固体に溶解度について解説していきます。固体の溶解度は、溶媒100gに溶ける溶質の質量(g)です。この定義は厳格に守られているので、必ず覚えておきましょう。固体の溶解度は、温度が上昇するとともに大きくなる傾向にあります。
固体の溶解度の計算では、2種類の公式のを用います。(溶質の質量)/(溶媒の質量)が一定となることと、(溶質の質量)/(溶液の質量)が一定となることです。現在注目している溶液と溶解度の情報との間でこの式を立て、計算していきます。
溶解度曲線
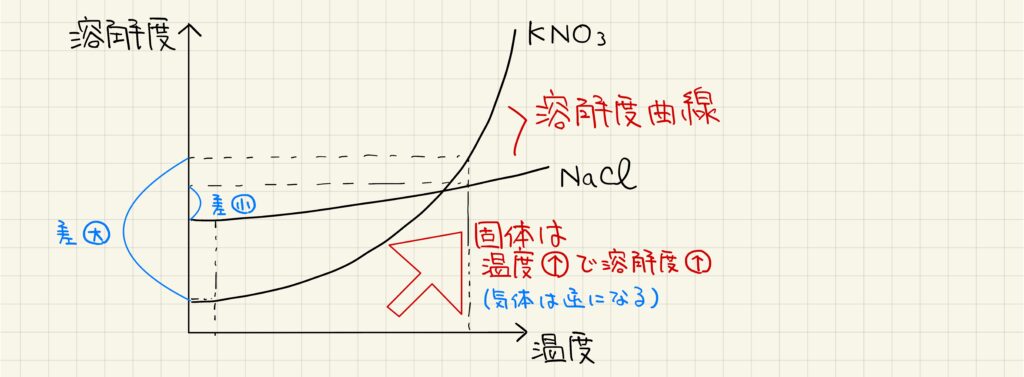
先述したように、固体の溶解度は温度上昇に従って大きくなります。この変化を表したものが溶解度曲線です。物質によって溶解度曲線の傾きは異なり、例えば塩化ナトリウムでは温度によってあまり溶解度が変化しませんが、硝酸カリウムは温度によって溶解度が大きく変化します。
再結晶法
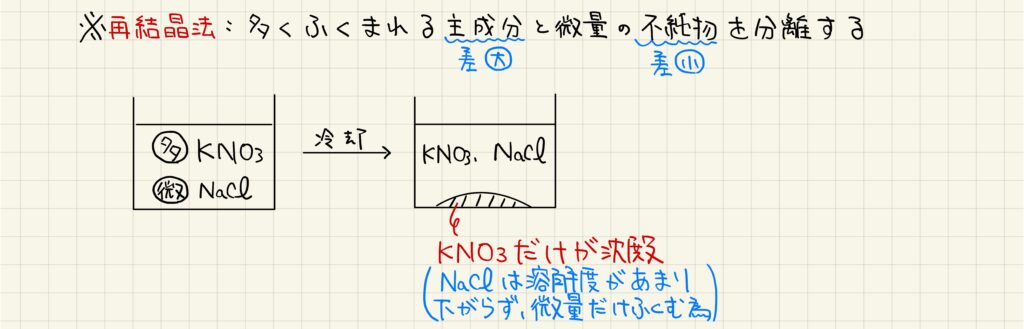
温度による溶解度変化の違いを利用して、物質を分離する方法があります。これを再結晶または再結晶法と呼びます。例えば、多量の硝酸カリウムが溶解した水溶液に、不純物として塩化ナトリウムが溶解しているとします。この溶液を冷却していくと、塩化ナトリウムは溶解度があまり変化しないため析出しませんが、硝酸カリウムは溶解度が小さくなって析出してきます。この操作により、混合物から純粋な硝酸カリウムを取り出すことができます。













