今回のまとめ

このページでは、気体に関するグラフについて解説していきます。前半は理想気体のグラフで、液化しない気体と液化する気体に分けて考えていきます。液化する気体では飽和蒸気圧に注意してグラフの概形を理解することが重要です。後半では、実在気体のグラフについて考えていきます。圧縮係数がどのように変化するのか見ていきましょう。
気体のグラフ
液化しない気体
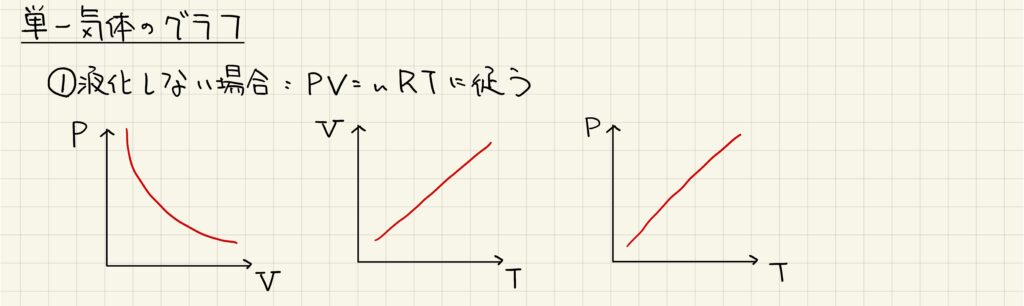
まず初めに、液化しない理想気体について見ていきましょう。全て状態方程式に従うので、2つの変数以外を定数とみなしてグラフを考えていきます。ボイルの法則に従い、圧力と体積は反比例の関係になります。また、シャルルの法則に従い、体積と温度は比例関係になります。最後に圧力と温度も比例関係になります。
液化する気体
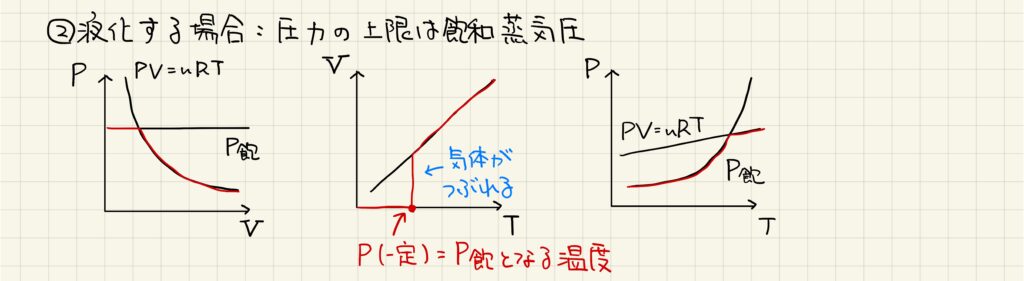
次に、液化する気体のグラフについて見ていきましょう。液化する気体では、温度に依存して変化する飽和蒸気圧が最大圧力であることに注意しなければなりません。
したがって、P-Vグラフでは圧力を大きくしていった時に飽和蒸気圧が上限となります。P-Tグラフも同様で、温度が低い状態では状態方程式に従わず、蒸気圧曲線に従って圧力が変化していきます。V-Tグラフにおいては定圧容器の変化を想像することが重要です。一定に保っている圧力が飽和蒸気圧と等しくなったとき、気体が外圧に押しつぶされて一気に体積が0になります。
圧縮係数のグラフ
圧縮係数とは
実在気体のグラフについて学習していきましょう。実在気体において、(PV)/(RT)の値を圧縮係数として定義して、理想気体からのズレを検討することができます。理想気体においては状態方程式が成立するので、圧縮係数の値は1になります。
分子間力は実在気体の圧力を小さくするので、圧縮係数の値を小さくします。したがって、分子間力が大きい分子では圧縮係数のグラフが大きく下に沈むことになります。また、分子自身の体積は実在気体の体積を大きくします。したがって、大きな分子ほど圧縮係数のグラフが大きく上昇することになります。低圧にするほど気体の体積が大きくなり、分子間力の影響と分子自身の体積の影響が小さくなるので、実在気体が理想気体に近くなります。
温度による圧縮係数の比較
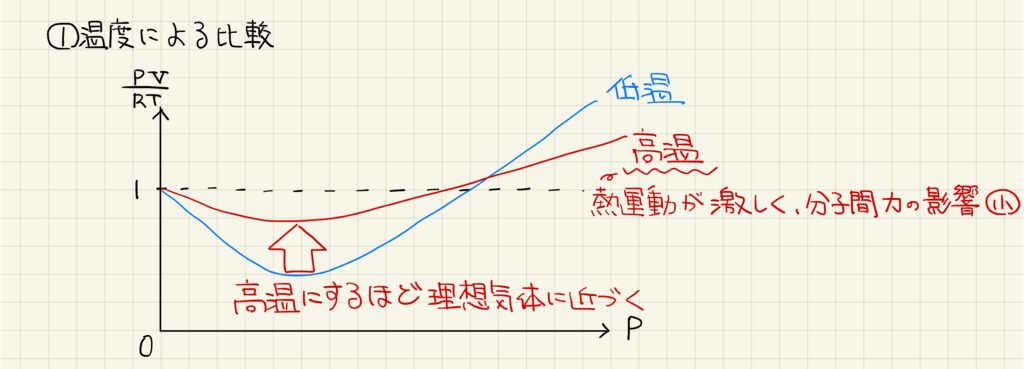
温度を変化させると、圧縮係数のグラフも変化します。実在気体は高温にするほど理想気体に近づくので、高温のグラフの方が圧縮係数が1に近くなります。
分子の種類による圧縮係数の比較
分子の種類を変化させると、圧縮係数のグラフも変化します。例えば、水素分子は無極性分子で分子量が小さく、表面積も小さいです。したがって、分子間力や分子自身の体積の影響が小さく、理想気体に近くなります。一方、アンモニア分子は極性分子で、分子量・表面積がある程度大きいので、理想気体とは異なる挙動を示します。その結果、水素分子の圧縮係数は1に近く、アンモニア分子の圧縮係数は1から大きく離れることになります。













