今回のまとめ

このページでは、実在気体の性質について解説していきます。高校化学では一般的に理想気体の計算問題が出題されますが、実在気体に関する問題もわずかに存在します。理想気体と実在気体の違いや、実在気体ならではの問題について見ていきましょう。
理想気体と実在気体
実在気体とは、実世界に存在している気体そのものを指します。一方で、理想気体とは実在気体の中で誤差となりうる要素を排除して計算しやすくしたもので、基本的には気体は理想気体として計算を行います。理想気体と実在気体の違いは大きく2つで、分子間力の有無と分子自身の体積の有無です。理想気体では分子間力と分子自身の体積については無視して考えますが、実在気体ではどちらも考慮する必要があります。
ファンデルワールスの状態方程式
分子間力の影響
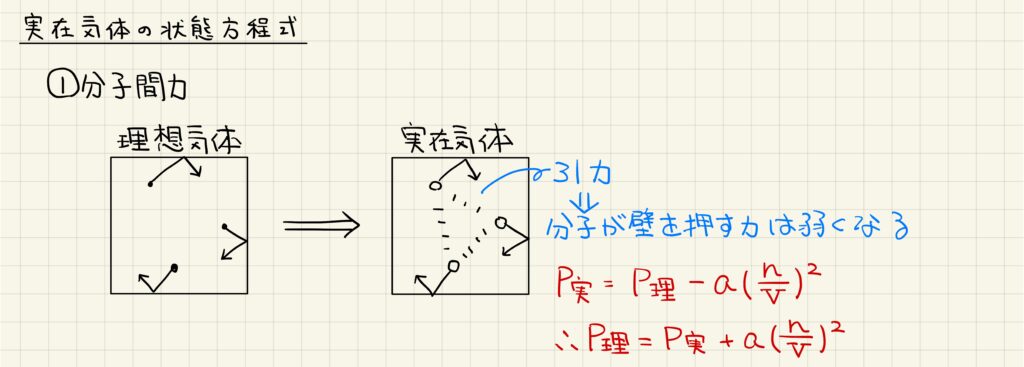
実在気体では、計算を行う際に分子間力の影響を考慮する必要があります。気体の圧力とは気体分子が容器の壁を押す力ですが、分子間力は気体分子同士を引き付けるので、これによって圧力が弱くなります。以上より、P実=P理ーa(n/V)2と表すことができます。ここで言うaは分子間力の大きさを示す定数です。また、分子間力は2つの分子が出会うことで生じるので、その影響は濃度の2乗に比例します。
分子間力の状態方程式への反映

先述したように、式中のaは分子間力の大きさを表します。分子間力にはファンデルワールス力と水素結合がありますが、このうちファンデルワールス力は分子の極性・分子量・表面積に依存しています。分子の極性・分子量・表面積が大きくなると、aの値も大きくなります。
分子自身の体積の影響
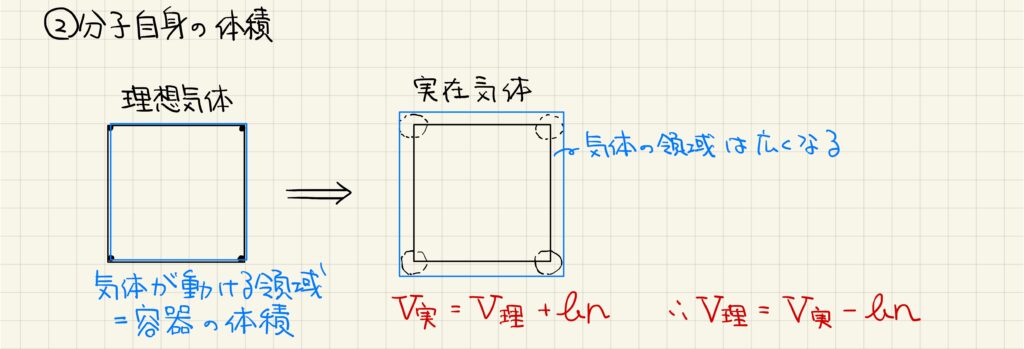
実在気体では、気体自身の体積を考慮する必要があります。理想気体の場合では気体分子の体積がないため、容器の体積と気体分子が動ける領域の体積が等しくなっていました。しかし、実在気体では気体分子自身の体積が存在するため、仮想的に容器よりも大きな領域を移動していることになります。以上より、V実=V理+bnと表すことができます。
分子自身の体積の状態方程式への反映
先述した式中で、bは気体分子の大きさを示します。例えばメタンとデカンを比較すると、炭素数からメタンの方が分子として小さいことは明らかです。したがって、bの値はメタンについて計算するときの方が小さくなります。
また、気体自身の体積の影響は物質量に比例します。ある気体分子1つが存在することで、他の気体分子はその周りに侵入できなくなります。この領域の大きさを排除体積と呼びます。排除体積の大きさは、(4/3)πr3×4で表されます。
ファンデルワールスの状態方程式

以上を総合して、実在気体において用いることができる状態方程式を導きましょう。ここまでで得られた式を変形して、理想気体の状態方程式に代入します。すると、分子間力の影響と気体自身の体積の影響を考慮した状態方程式が立てられます。これをファンデルワールスの状態方程式と呼びます。実在気体の計算においては、この式を用いて行うことが多いです。













