このページのまとめ
学習のポイント
- 金属結晶の単位格子には、面心立方格子・体心立方格子・六方最密構造の3種類がある。
- 面心立方格子中には正味4個の原子が含まれ、充填率は74%である。
- 体心立方格子中には正味2個の原子が含まれ、充填率は68%である。
- 六方最密構造の単位格子中には正味2個の原子が含まれ、充填率は74%である。
まとめノート
このページでは、金属結晶の単位格子について解説していきます。金属結晶の単位格子では、面心立方格子・体心立方格子・六方最密構造の3種類があります。それぞれの結晶構造について、正味の数・配位数・充填率・密度に関して学習していきます。充填率の計算では断面を取ることが重要ですので、よく確認していきましょう。
金属結晶の結晶格子
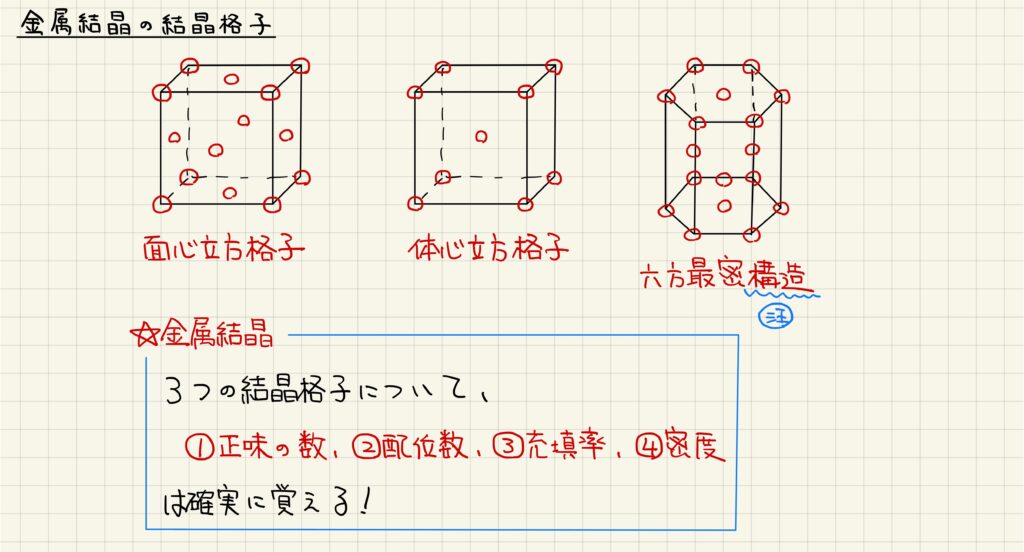
先述したように、金属結晶の単位格子には面心立方格子・体心立方格子・六方最密構造の3種類があります。常温の金属結晶がとりうる結晶構造はこの3種類のみで、必ずいずれかの単位格子をとっています。六方最密構造のみ、単位格子が立方体ではないので語尾が「構造」となっていることに注意しましょう。金属結晶に関して、正味の数・配位数・充填率・密度を学習していきましょう。
面心立方格子
正味の数・配位数

面心立方格子は、立方体の頂点と面の中心に粒子が配置した構造です。頂点の粒子は8個の立方体と共有されているので、正味1/8球としてカウントします。面の中心にある粒子は2個の立方体と共有されているので、正味1/2球としてカウントします。合計すると、面心立方格子の正味の数は4個です。
配位数とは、ある原子が接する他の原子の数です。単位格子を2つ並べるとわかりやすいですが、面心立方格子において配位数は12個になります。
充填率
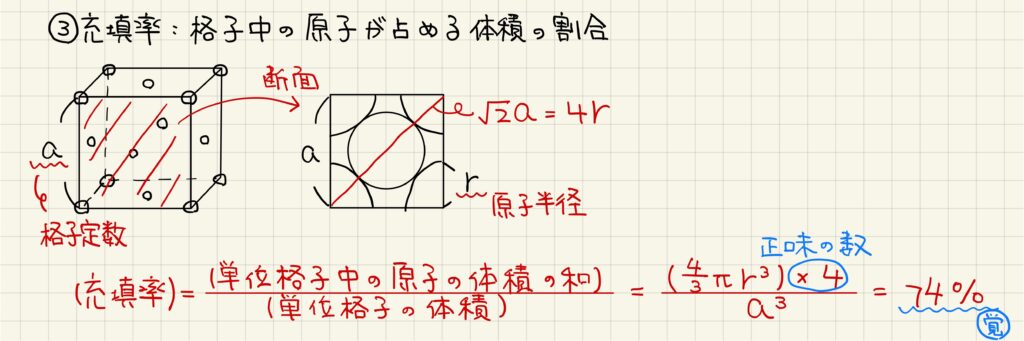
充填率とは、単位格子の体積に対して粒子が占める体積の割合です。単位格子の立方体の一片の長さを、格子定数と呼びます。粒子同士が接する面で断面をとることで、格子定数と粒子半径の関係を求めることができます。面心立方格子では、√2a=4rとなります。球1つの体積は4/3×π×r3で表されるので、充填率は74%となります。この数字は頻繁に出てくるので、覚えておいても良いでしょう。
密度

密度は、単位格子の体積に対する粒子の重さの比になります。単位格子の密度を計算する際には、アボガドロ数や原子量、正味の数を用いて計算します。
体心立方格子
正味の数・配位数

体心立方格子は、立方体の頂点と立方体の中心に粒子が位置しています。正味の数としては、全部で2個になります。また、配位数は中心の粒子から見るとわかりやすいですが、8個となります。
充填率・密度
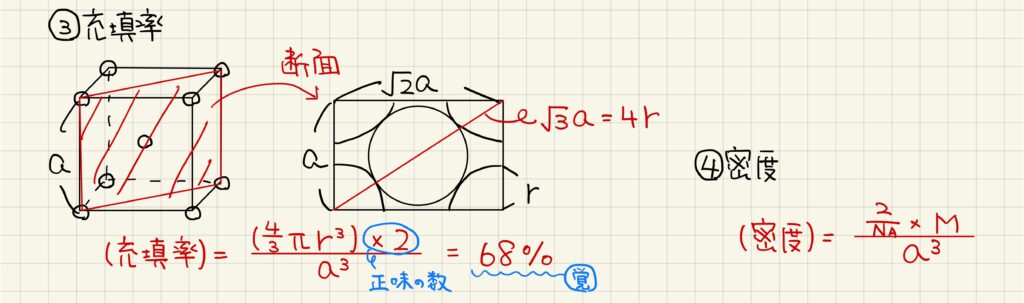
体対角で面をとることで、格子定数と粒子半径の関係を求めることができます。体心立方格子の場合は、√3a=4rという関係になります。これを充填率の公式に代入して計算すると、体心立方格子の充填率は68%となります。
密度に関しては、面心立方格子と同様に考えれば計算することができます。体心立方格子ととる構造であればどの元素でも充填率は変わりませんが、原子量によって密度は変化します。
六方最密構造
正味の数・配位数
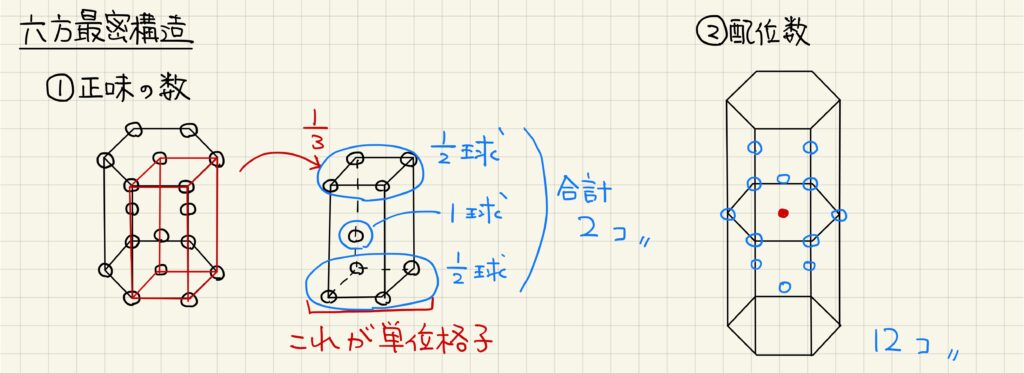
六方最密構造は、六角柱の形で表されることが多いですが、単位格子はその3分の1の四角柱です。正味の数を計算すると、全部で2個となります。六角柱を縦に2つ並べて考えると、配位数が12であることが分かりやすいです。
充填率・密度

六方最密構造では、粒子同士が正四面体の構造に並んでいます。格子定数が正四面体の一辺の長さになっているので、ここから格子定数と粒子半径の関係を求めることができます。六方最密構造では、a=2rとなります。これまでと同様に充填率を計算すると、充填率は74%となります。この充填率は面心立方格子と同じです。密度に関しては、六角柱の体積を使って計算することができます。













