浸透圧

管理人

今回のまとめ

このページでは、浸透圧の問題について解説していきます。浸透圧の問題では、力のつり合いの式とファントホッフの式という２つの重要な公式があります。これらを使いこなすことで問題を簡単に解くことができますから、両者しっかりと理解していきましょう。

浸透の仕組み
1. エントロピー増大の法則
2. U字管を用いた浸透現象
力のつり合い
ファントホッフの式

浸透の仕組み

エントロピー増大の法則

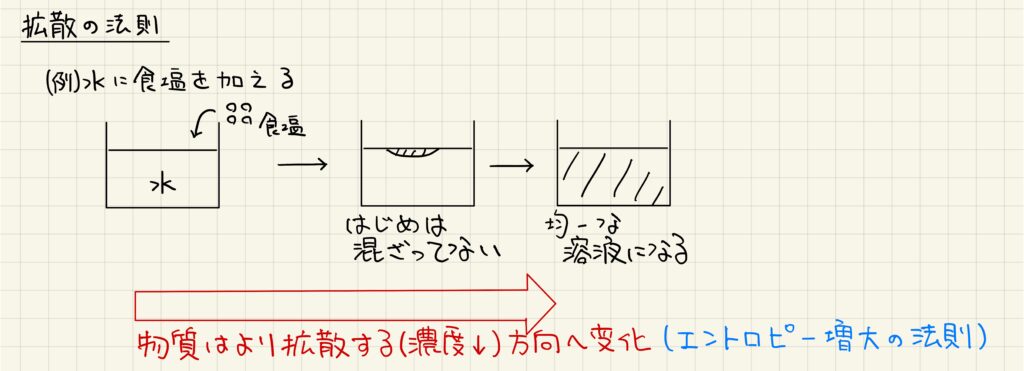
浸透という現象は、エントロピー増大の法則によって説明することができます。例えば純水に食塩を加えた場合、はじめは局所的に濃度が高い食塩水ができますが、かき混ぜなくても自然と一様な食塩水ができあがります。このように、物質がより拡散しようとする働きをエントロピー増大の法則と呼びます。

U字管を用いた浸透現象

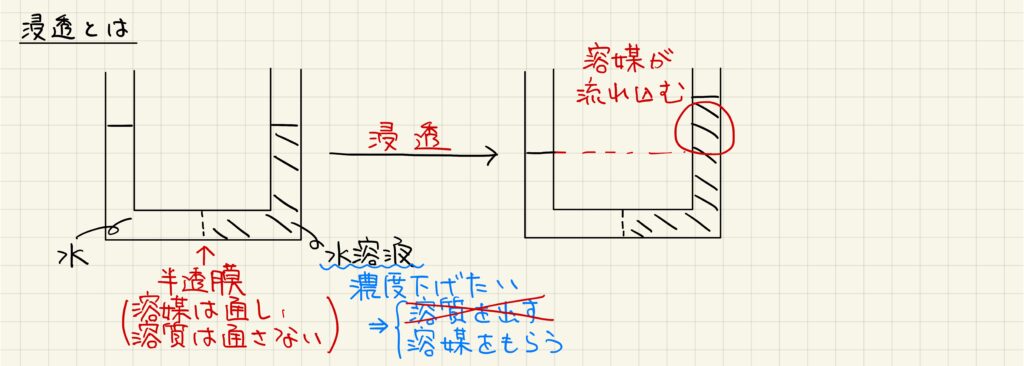
では次に、U字管を用いて浸透現象を観察していきましょう。U字管の中心を半透膜（溶媒は通して溶質は通さない膜）で仕切り、左側に純水、右側に水溶液を加えた場合を想定してみます。このとき、エントロピー増大の法則より、水溶液は拡散したい（濃度を下げたい）状態にあります。このとき、溶質は半透膜を通過できませんから、溶媒が溶液側に引き込まれることになります。これが浸透現象で、溶液側の体積が大きくなります。

力のつり合い

先程と同様に、U字管を使って浸透圧を考えていきましょう。エントロピー増大の法則にしたがって浸透が起きた後、しばらくすると溶媒の移動が止まったように見えます。これは、溶媒を引き込もうとする浸透圧と、上に突き出た液柱の圧力とがつり合ったためです。このときの水溶液の密度をd(g/cm³)U字管における液面差をh(cm)とすると、浸透圧πは密度dで高さhの液柱が示す圧力と等しいことが分かります。

次に、大気圧を求めるトリチェリーの実験を思い出してみましょう。この実験では、大気圧と水銀柱の圧力がつり合っています。つまり、密度13.6g/cm³で高さ76cmの液柱は1atmの圧力を示すことが分かります。

以上を比較すると、浸透圧πは、大気圧から比例計算で求めることができます。これが浸透圧の問題でよく用いられる力のつり合いの式です。

ファントホッフの式

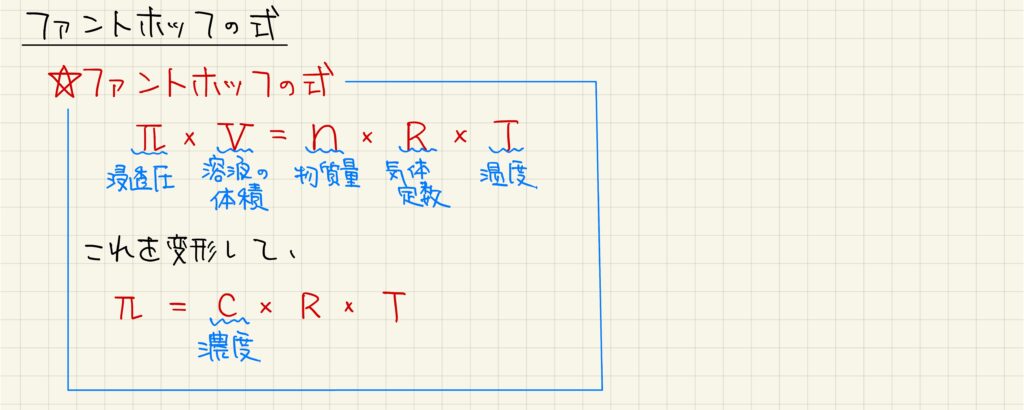
次に、ファントホッフの式について学習していきます。ファントホッフの式は、πV＝ｎRTで表されます。気体の状態方程式と形が似ているので、覚えやすいです。また、溶液の体積が正確にわからない場合でもπ＝CRTという形で計算することもできます。ここで示すπは円周率ではなく、浸透圧を表していることに注意しておきましょう。

体積に関する注意

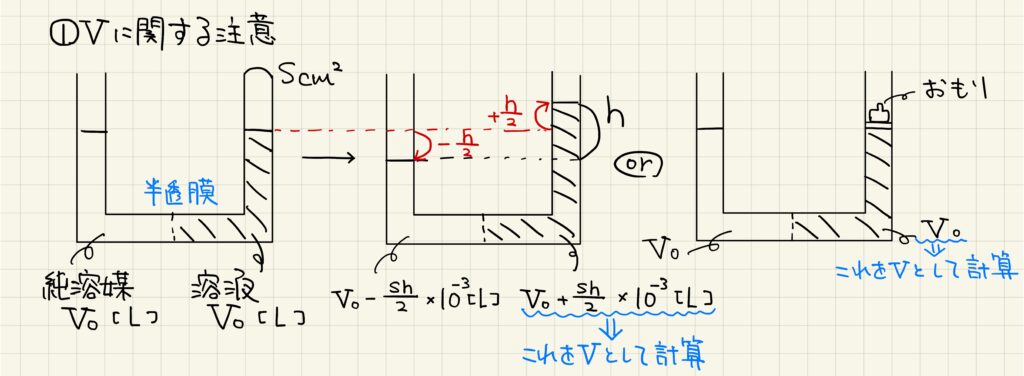
ファントホッフの式を使うにあたって、いくつか注意点があります。まずは体積についてです。先程の例と同様にU字管を用いて浸透現象を観察し、液面差h(cm)ができたとします。このとき、実際には、左側の液柱がh/2だけ下がって、右側の液柱がh/2だけ上がることで、合計してhの液面差ができています。すなわち、水溶液のもとの体積をV₀(L)、U字管の表面積をS(cm²)とすると、浸透が止まったあとの溶液の体積はV₀+{(Sh)/2}×10^-3(L)であり、これをファントホッフの式のVとして計算する。このように、ファントホッフの式では浸透が止まった段階での溶液の体積を用いて計算しなければならない点に注意しよう。